AFRL x UNM Agile Manufacturing Laboratory

Who Are We?

At the UNM Agile Manufacturing Laboratory, we spearhead transformative research at the intersection of cutting-edge technologies and space exploration. Explore our diverse expertise encompassing orbital robotics, agile manufacturing, smart satellite development, and the frontier of In-Orbit Servicing, Assembly, and Manufacturing (ISAM) as we strive to redefine the possibilities of space innovation.

Research Interests

Orbital Robotics

Our focus lies in developing intelligent robotic systems designed for precision and adaptability in the challenging environment of outer space.

Agile Manufacturing

Our research explores dynamic and responsive manufacturing processes, optimizing efficiency and adaptability.

Smart Satellite Development

We aim to revolutionize satellite capabilities by integrating state-of-the-art technologies, including artificial intelligence and advanced communication systems.

In-Orbit Servicing, Assembly, and Manufacturing (ISAM)

Our focus is on developing technologies and strategies that enable tasks such as satellite assembly, repair, and manufacturing in space.

Recent Research Highlights

AirBender: Adaptive Transportation of Bendable Objects Using Dual UAVs

The interaction of robots with bendable objects in midair presents significant challenges in control, often resulting in performance degradation and potential crashes, especially for aerial robots due to their limited actuation capabilities and constant need to remain airborne. This letter presents an adaptive controller that enables two aerial vehicles to collaboratively follow a trajectory while transporting a bendable object without relying on explicit elasticity models. Our method allows on-the-fly adaptation to the object’s unknown deformable properties, ensuring stability and performance in trajectory-tracking tasks. We use Lyapunov analysis to demonstrate that our adaptive controller is asymptotically stable. Our method is evaluated through hardware experiments in various scenarios, demonstrating the capabilities of using multirotor aerial vehicles to handle bendable objects.

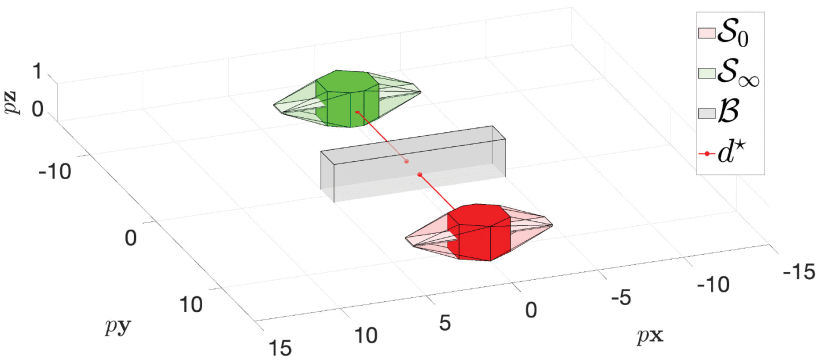
Safe Vehicle Motion Planning Using Constraint Admissible Positive Invariant Sets on SE(3)

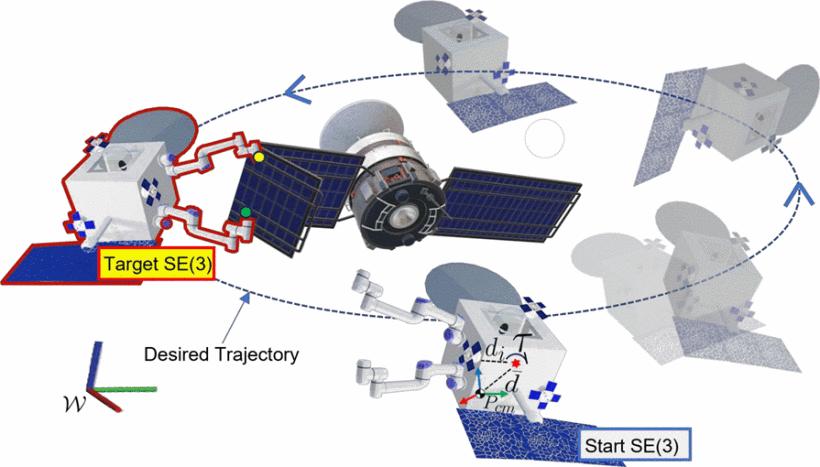
This letter extends the application of the invariant set motion planner (ISMP) to space vehicles operating in SE(3)=SO(3)⋊R3 , considering the quaternion representation of SO(3) . We provide a proof for a collision-free set by extending the concepts of configuration-space bubbles from robotics literature. We derive a constraint admissible positive invariant (CAPI) subset within the configuration-space bubble for a robust linearization of the nonlinear vehicle dynamics. The motion planner constructs a directed graph of position and orientation equilibria covering SE(3) . CAPI sets are constructed to verify that equilibria are connected by a feasible trajectory. Graph search is applied to determine a sequence of reference configurations, starting at an initial position-orientation and terminating at a goal position-orientation. Simulation results are included that demonstrate the safe navigation of a vehicle in the presence of an obstacle. The trajectory is shown to maintain the CAPI conditions and is therefore safe under the nonlinear translational and rotational closed-loop vehicle dynamics.

Adaptive Robot Detumbling of a Non-Rigid Satellite

The challenge of satellite stabilization, particularly those with uncertain flexible dynamics, has become a pressing concern in control and robotics. These uncertainties, especially the dynamics of a third-party client satellite, significantly complicate the stabilization task. This paper introduces a novel adaptive detumbling method to handle non-rigid satellites with unknown motion dynamics (translation and rotation). The distinctive feature of our approach is that we model the non-rigid tumbling satellite as a two-link serial chain with unknown stiffness and damping in contrast to previous detumbling research works which consider the satellite a rigid body. We develop a novel adaptive robotics approach to detumble the satellite by using two space tugs as servicer despite the uncertain dynamics in the post-capture case. Notably, the stiffness properties and other physical parameters, including the mass and inertia of the two links, remain unknown to the servicer. Our proposed method addresses the challenges in detumbling tasks and paves the way for advanced manipulation of non-rigid satellites with uncertain dynamics.

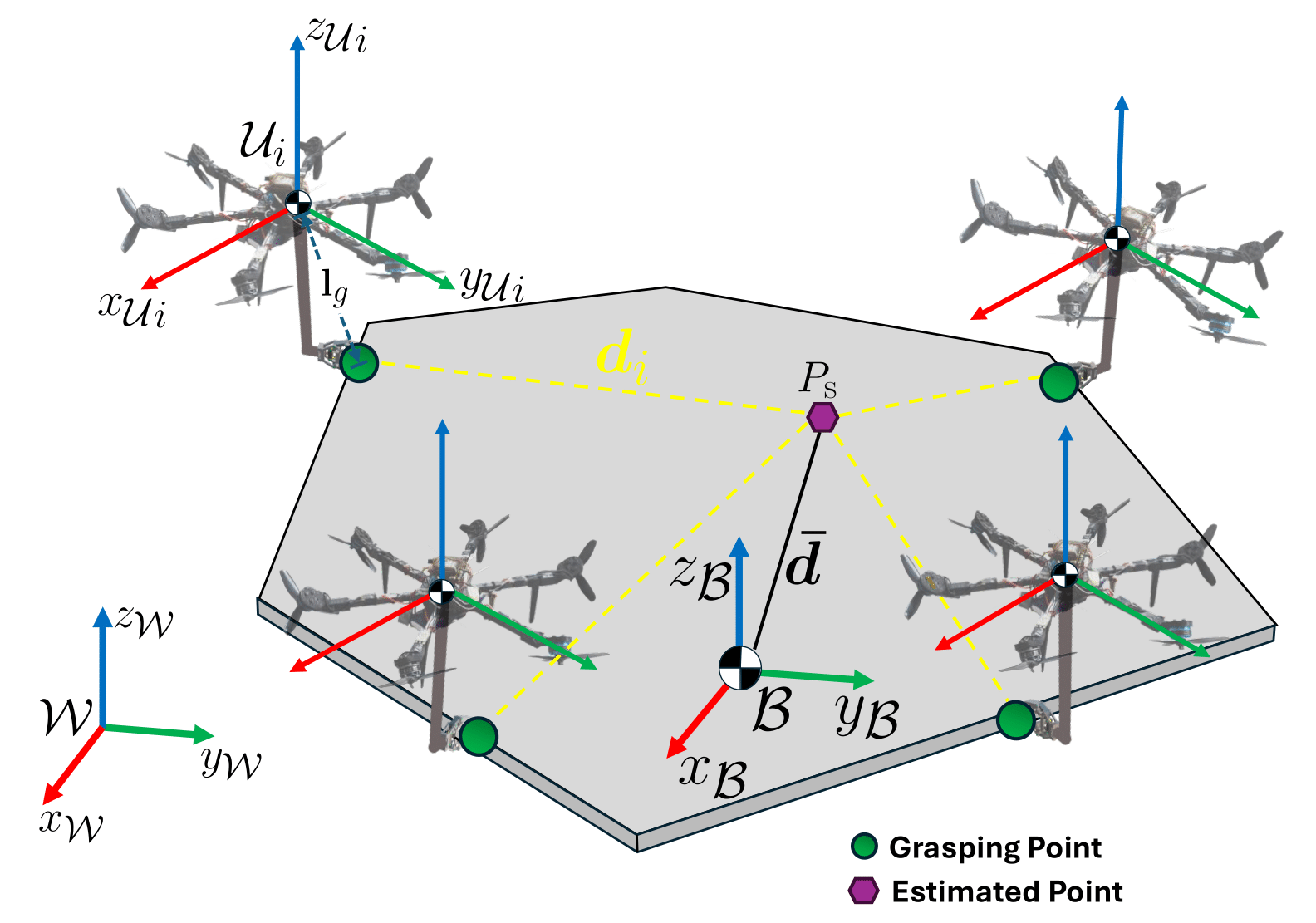
Decentralized adaptive aerospace transportation of unknown loads using a team of robots

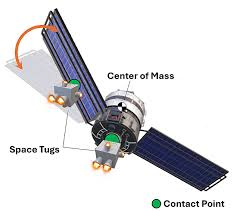
Transportation missions in aerospace are limited to the capability of each aerospace robot and the properties of the target transported object, such as mass, inertia, and grasping locations. We present a novel decentralized adaptive controller design for multiple robots that can be implemented in different kinds of aerospace robots. Our controller adapts to unknown objects in different gravity environments. We validate our method in an aerial scenario using multiple fully actuated hexarotors with grasping capabilities, and a space scenario using a group of space tugs. In both scenarios, the robots transport a payload cooperatively through desired three-dimensional trajectories. We show that our method can adapt to unexpected changes that include the loss of robots during the transportation mission.

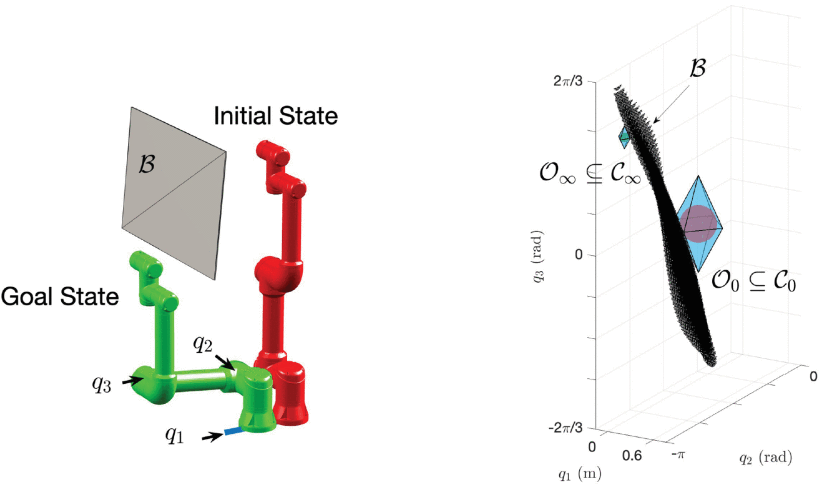
Safe Motion Planning for Serial-Chain Robotic Manipulators via Invariant Sets

Ongoing research is focused on developing autonomous motion-planning algorithms capable of addressing nonlinear robot manipulator dynamics and non-convex collision avoidance constraints. This letter extends the application of the invariant-set motion planner (ISMP) to robot motion planning. We broaden the proof of output admissibility for configuration-space bubbles, accommodating robots with both prismatic and revolute joints. We derive a constraint admissible positive invariant (CAPI) subset within the configuration-space bubble for closed-loop system dynamics, integrating proportional-derivative joint controllers. Furthermore, we outline conditions for CAPI sets to be input admissible. Utilizing random exploring tree techniques, we identify a sequence of CAPI sets to guide the robot from an initial configuration to a goal equilibrium state while avoiding collisions. We illustrate the effectiveness and feasibility of the ISMP through a simulation involving the Universal Robots UR5e mounted on an actuated rail, modeled as a prismatic joint. Simulation results validate that ISMP for robot motion planning.

Autonomous Multi-Robot Servicing for Spacecraft Operation Extension

This paper considers the robotic on-orbit servicing of a client satellite. We present an adaptive robotic system to perform two on-orbit tasks: client manipulation and jammed component dislodging (e.g., a solar panel). We use adaptive control due to the uncertainty of the client dynamics and the stiffness of the jammed component. We present two methods for dislodging: a decentralized approach with multiple free-fiying collaborating agents and then transferring the same decentralized approach to a multi-robot arms system. We present simulation studies for these on-orbit servicing tasks. These studies validate the effectiveness of the presented controller despite uncertainty and unmodeled dynamics, such as nonlinear friction.

Meet our Research Team